研究者総覧「情報知」
複雑系科学専攻
- 氏 名
- 安田 耕二(やすだ こうじ)
- 講座等
- 情報可視化論講座
- 職 名
- 准教授
- 学 位
- 博士(工学)
- 研究分野
- 量子化学 / 生体関連分子 / 専用計算機

研究内容
巨大分子の理論化学シミュレーション
■研究の概要■
自然界の化学現象、特に分子や分子集合体、生体関連分子の構造や性質を、計算機で予測・シミュレーションするための、新しい理論化学手法と計算機の開発を推進している。これまでに、密度行列を用いた量子化学手法や、理論的に導かれた量子力学/分子力学(QM/MM)法を提案、開発してきた。最近では、SIMD型超並列専用計算機上での、理論化学シミュレーションの実現を目指している。
■研究テーマ■
(1) 密度行列を用いた新しい量子化学手法の開発
物質の性質を理論的に予測する、新しい量子化学手法の開発を行っている。物質中の電子の運動は、波動方程式の解である波動関数により定まるが、電子間斥力のため、正確な波動関数を求める事はほぼ不可能と思われている。この世界には2体力しか存在しないので、波動関数より簡単な縮約密度行列や電子密度も、波動関数と同じ情報を含む。この事実に立脚した密度行列理論、密度汎関数理論を開発している。後者は第一原理シミュレーションで現在広く使われているが、多体問題の難しさを複雑な汎関数を導入して消去しようとするため、汎関数の決定が本質的に難しい。我々は密度行列の反対称条件や、交換相関エネルギー汎関数を場の理論により系統的に求める方法を示し、具体的な汎関数の一例を与えた。これらの新しい方法は、分子や固体、表面の構造や反応を、正確かつ効率的に予測する新しい理論となると考えている。
(2) QM/MM法による生体分子のシミュレーション
蛋白質の構造科学の急速な発展から考えると、量子化学に基づく蛋白質の機能解析、特に酵素反応機構の解明が、近いうちに重要視されるのは間違いない。対象分子の大きさや、要求される計算精度等を考えると、重要部分のみ量子力学で、残りの部位は分子力学で扱う、いわゆる量子力学/分子力学(QM/MM)法が現実的で唯一の計算法である。この方法では量子系と古典系の接合点の扱い方が問題となる。経験的モデルが現在利用されているが、生体分子に要求されるエネルギー精度には遠く及ばず、計算結果が無意味になりかねない。我々は繰り込みによる自由度の消去という観点から、このQM/MM法を理論的に定め、これまでのQM/MM法に潜在していた非経験的要素を駆逐した。MM法で記述される古典部分に電子系の量子統計状態を対応させ、実現確率の高い状態のみを考慮する事で、密度行列繰り込み群と類似の方法でQM/MM法を導き、量子/古典系の接合点を定めた。化学反応では副次的な蛋白質の大部分を圧縮して表現する事で、高速かつ高精度に巨大分子のシミュレーションが可能となり、理論化学と構造生物学に新しい接点ができる。
(3) SIMD型超並列計算機上での理論化学の実現
理論化学では高性能計算機により、巨大分子を高精度に扱えるようになった。近年の計算機は高速な内部動作速度と多段パイプラインが特徴であり、外部記憶との速度差を解消するための高速メモリーや、正確な分岐予測機構を必要とする。そのためCPUのかなりの素子が、これらのメモリー等に使われる。定型的浮動小数演算を専ら行う科学技術計算では、メモリー等の代わりに単純な演算機を数千個以上集積した、超並列SIMD計算機により、飛躍的な性能増加が見込まれる。共同研究者の戎崎(理研)や牧野(東大)らを中心に現在開発されている、この超並列SIMD計算機上で、理論化学シミュレーションを実行する研究をしている。この超並列SIMD計算機の各CPUに局所メモリーは無く、CPU間は疎結合で通信速度は小さいため、細粒度の並列性が必要である。このアーキテクチャは、現在使われている共有又は分散メモリー型の並列計算機と大きく異なり、全く新しいアルゴリズムで理論化学シミュレーションを実装する必要がある。これらを順に開発しており、ここ数年以内で、単体で数テラFLOPSの性能の専用計算機上で、理論化学シミュレーションが実行できる予定である。
自然界の化学現象、特に分子や分子集合体、生体関連分子の構造や性質を、計算機で予測・シミュレーションするための、新しい理論化学手法と計算機の開発を推進している。これまでに、密度行列を用いた量子化学手法や、理論的に導かれた量子力学/分子力学(QM/MM)法を提案、開発してきた。最近では、SIMD型超並列専用計算機上での、理論化学シミュレーションの実現を目指している。
■研究テーマ■
(1) 密度行列を用いた新しい量子化学手法の開発
物質の性質を理論的に予測する、新しい量子化学手法の開発を行っている。物質中の電子の運動は、波動方程式の解である波動関数により定まるが、電子間斥力のため、正確な波動関数を求める事はほぼ不可能と思われている。この世界には2体力しか存在しないので、波動関数より簡単な縮約密度行列や電子密度も、波動関数と同じ情報を含む。この事実に立脚した密度行列理論、密度汎関数理論を開発している。後者は第一原理シミュレーションで現在広く使われているが、多体問題の難しさを複雑な汎関数を導入して消去しようとするため、汎関数の決定が本質的に難しい。我々は密度行列の反対称条件や、交換相関エネルギー汎関数を場の理論により系統的に求める方法を示し、具体的な汎関数の一例を与えた。これらの新しい方法は、分子や固体、表面の構造や反応を、正確かつ効率的に予測する新しい理論となると考えている。
(2) QM/MM法による生体分子のシミュレーション
蛋白質の構造科学の急速な発展から考えると、量子化学に基づく蛋白質の機能解析、特に酵素反応機構の解明が、近いうちに重要視されるのは間違いない。対象分子の大きさや、要求される計算精度等を考えると、重要部分のみ量子力学で、残りの部位は分子力学で扱う、いわゆる量子力学/分子力学(QM/MM)法が現実的で唯一の計算法である。この方法では量子系と古典系の接合点の扱い方が問題となる。経験的モデルが現在利用されているが、生体分子に要求されるエネルギー精度には遠く及ばず、計算結果が無意味になりかねない。我々は繰り込みによる自由度の消去という観点から、このQM/MM法を理論的に定め、これまでのQM/MM法に潜在していた非経験的要素を駆逐した。MM法で記述される古典部分に電子系の量子統計状態を対応させ、実現確率の高い状態のみを考慮する事で、密度行列繰り込み群と類似の方法でQM/MM法を導き、量子/古典系の接合点を定めた。化学反応では副次的な蛋白質の大部分を圧縮して表現する事で、高速かつ高精度に巨大分子のシミュレーションが可能となり、理論化学と構造生物学に新しい接点ができる。
(3) SIMD型超並列計算機上での理論化学の実現
理論化学では高性能計算機により、巨大分子を高精度に扱えるようになった。近年の計算機は高速な内部動作速度と多段パイプラインが特徴であり、外部記憶との速度差を解消するための高速メモリーや、正確な分岐予測機構を必要とする。そのためCPUのかなりの素子が、これらのメモリー等に使われる。定型的浮動小数演算を専ら行う科学技術計算では、メモリー等の代わりに単純な演算機を数千個以上集積した、超並列SIMD計算機により、飛躍的な性能増加が見込まれる。共同研究者の戎崎(理研)や牧野(東大)らを中心に現在開発されている、この超並列SIMD計算機上で、理論化学シミュレーションを実行する研究をしている。この超並列SIMD計算機の各CPUに局所メモリーは無く、CPU間は疎結合で通信速度は小さいため、細粒度の並列性が必要である。このアーキテクチャは、現在使われている共有又は分散メモリー型の並列計算機と大きく異なり、全く新しいアルゴリズムで理論化学シミュレーションを実装する必要がある。これらを順に開発しており、ここ数年以内で、単体で数テラFLOPSの性能の専用計算機上で、理論化学シミュレーションが実行できる予定である。
■今後の展開■
上述の3要素を結合する事で、現在より飛躍的に高速、高精度、大規模な理論化学シミュレーションが、誰でも安価に、近い将来実現可能になる。純粋な自然科学に貢献するのみならず、ナノテク、材料設計、構造生物学、創薬などにも広く使われると考えている。
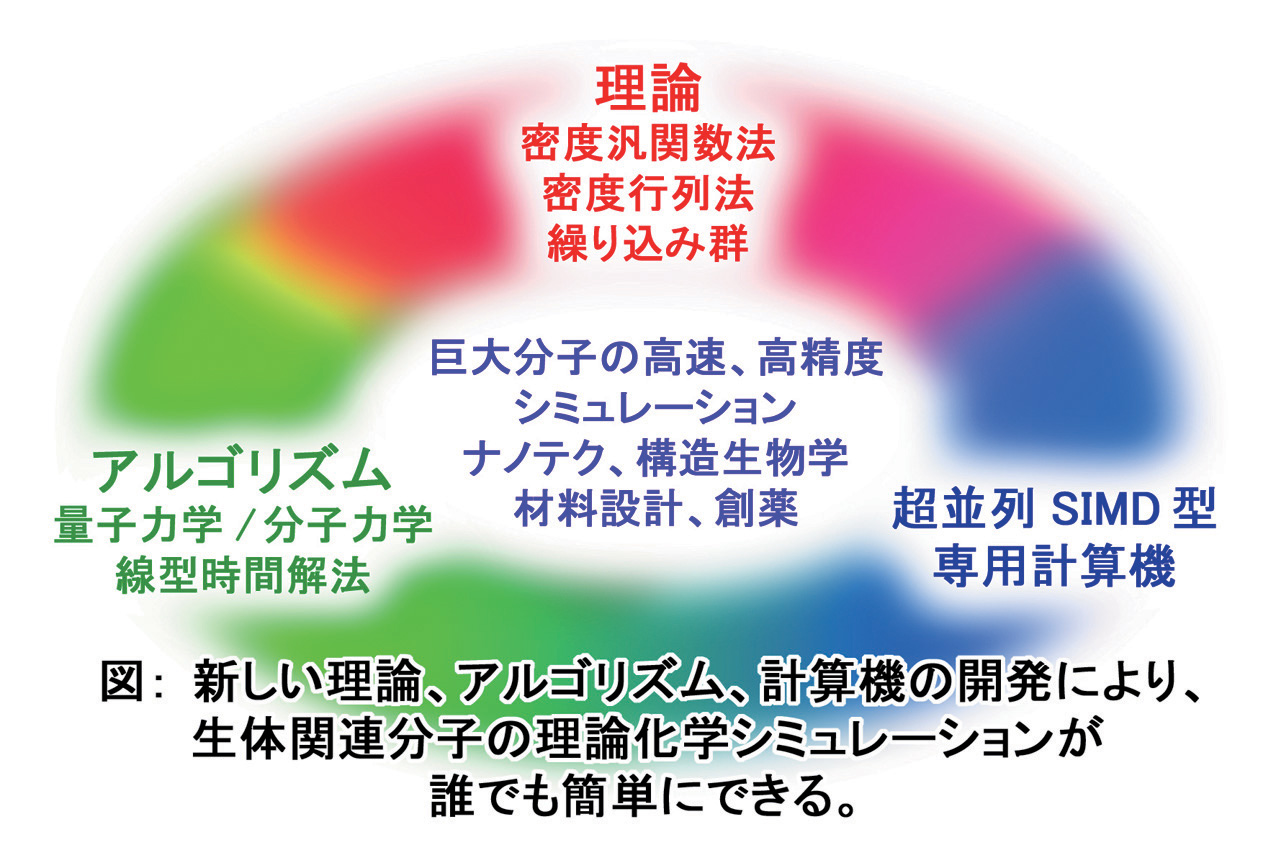
巨大分子の理論化学シミュレーション
経歴
- 1997年京都大学大学院工学研究科合成・生物化学専攻博士後期課程修了。博士(工学)。
- 1997年名古屋大学大学院人間情報学研究科助手。現在に至る。
- 1994年より学術振興会特別研究員(1997年まで)。
所属学会
- 日本物理学会
主要論文・著書
- K. Yasuda and D. Yamaki, Simple minimum principle to derive a quantum-mechanical/molecular-mechanical method, Journal of Chemical Physics, 121 (9), 3964 (2004).
- Koji Yasuda, Local approximation of the correlation energy functional in the density matrix functional theory, Phys. Rev. Letters, 88 (5), 053001 (2002).
- Koji Yasuda, Correlation energy functional in the density matrix functional theory, Phys. Rev. A63, 032517 (2001).
- Comment on "Family of modified contracted Schroedinger equations"
- Size extensivity of the variational reduced-density-matrix method
- グラフィックボードで計算物理を
- Two-Electron Integral Evaluation on the Graphics Processor Unit
- Accelerating Density Functional Calculations with Graphics Processing Unit











