研究内容

多体系動力学の数理物理的研究

　［研究概要］
自然現象であれ社会現象であれ、すべての現象は微視的構成分子の集団運動によって形成される巨視的様相として捉えることができる。このような多体相互作用系に現れる様々な非線型・非平衡現象を物理的に研究し、共通するダイナミックスの数理的構造の解明を目指している。研究対象は、素粒子・スピン系や粉体などの物質的集団から、交通流・歩行者流・生物集団・ネットワークなどの社会的集団に及び、対象の違いに依存しない協同現象の力学の普遍性と多様性を探っている。方法としては、場の理論・くりこみ群・微差分方程式・力学系・量子系など数学的・統計物理的解析手法、及び計算機シミュレーションを併用している。
［研究テーマ］と［今後の展開］
(1) 場の理論及びくりこみ群の研究
素粒子場は多体相互作用により高エネギー現象や宇宙進化の過程を説明する。その解析方法は統計力学・力学系の手法と共通しており、私はくりこみ群の手法等を用いて、ゲージ場及び統計力学スピン系について研究を進めている。複素数化した結合定数に対するくりこみ群の周期点の構造に内在する高度の普遍性の存在をスピン系・ゲージ系について調べている。低次元での可解系の代数構造に関連して量子群のサイクリック表現が物理量にみられるフラクタル構造の背後にあると推測し、くりこみ群との関係についても調べている。こういった観点は、無限自由度系の相転移現象や場の理論に対する体系的理解や分類にあらたな道を拓くものである。
(2) 交通流の数理的研究
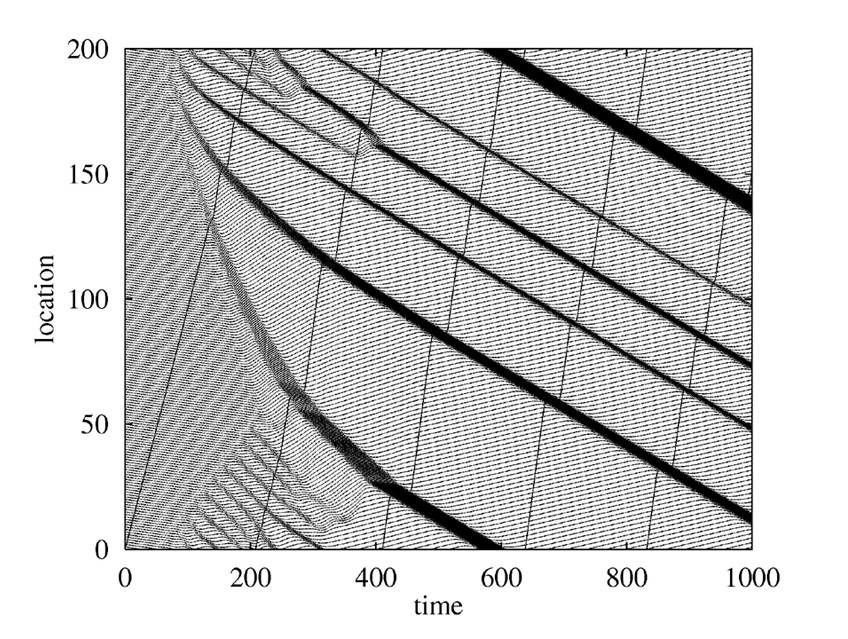
交通流は、非線形・非平衡的な性質を持つ複雑システムであり、数理的研究が可能な典型的な対象である。１次元系なのでシミュレーションだけでなく解析的研究も可能である。我々は新しい非線形模型（Optimal Velocity（OV）模型）を提案し、非線形相互作用の協力現象の結果として初めて動力学的なソリトン的な解として渋滞パターンの形成を再現した。これにより渋滞形成は非平衡多体系の相転移現象であるという観点を与え、粉体流など広い対象を含む非線型力学における分岐現象や散逸模型のパターン形成問題の研究であることを示した。理論的結果は現実のデータを非常に良く再現し、交通流の基礎模型としての地位を確立している。さらに現実のボトルネックにおける渋滞流は特徴的な“同期流”と呼ばれる非平衡現象が現れており、渋滞発生がsub-critical Hopfという転移現象であることより存在する不安定解がボトルネックにより安定化して現実に現れる、という力学系の側面からの研究を進めている。
(3) 多体相互作用散逸系の研究
OV模型と同じクラスにある時間遅れを含んだ一階微分方程式が渋滞クラスタ解を持ち、その厳密解が楕円関数で記述され、戸田格子の解と深い関係にあることを見出した。この微分差分方程式はロトカ-ヴォルテラ方程式の微分差分形と同じクラスにあり、散逸系のクラスタ解と保存系でのソリトン解との関連について理解を深めた。このシステムがソリトン系の基礎である戸田格子場と深い関係にあることを見出し、散逸系が自己組織化し可積分系となってソリトン的クラスタを出現するという、広範な複雑多体系の数理的研究における一つの視点を与えた。更に交通流を典型とする複雑システムの多体相互作用の研究は、粉体流、歩行者流や避難者流、生物集団の運動・形態形成、情報ネットワーク、社会的システムなどの動力学・相転移現象にも拡大し、研究を進めている。
(4) 自己駆動粒子集団の動力学の研究
交通流に始まった多体系流動現象の研究は、粉体流、避難者流、生物集団の運動、ネットワークの形成、経済など、物質的対象から生物・社会的な集団へと対象を拡大しており、「自己駆動粒子」（Self-Driven Particles）というエネルギー非保存系/散逸系における集団運動の動力学として統合的な概念で広範な対象を体系化しうる学問分野に成長しつつある。これは、従来の平衡系・保存系という単純な物質科学から、非平衡系・非保存系/散逸系という複雑な物質科学現象への発展のみならず、生命現象・社会現象につながる重要な科学概念を数理的に扱う研究に道を拓くものである。