研究者総覧「情報知」
計算機数理科学専攻
- 氏 名
- 金森 敬文(かなもり たかふみ)
- 講座等
- 計算論講座
- 職 名
- 教授
- 学 位
- 博士(学術)
- 研究分野
- 機械学習 / 数理統計学 / 最適化

研究内容
機械学習・数理統計学に関する理論的研究
■研究の概要■観測や調査によって得られるデータから、その背後にある構造について推論を行うことは、科学や工学、人文科学など広範囲に渡る分野において重要な課題である。データの生成過程は複雑で、実際にはノイズを含んでいることが多いため、確率的な構造を前提にしてデータの解析を行うことになる。データ解析の目的は多様であり、背後の確率構造を推定するための方法、将来のデータの予測のための手法、仮説の検証のための検定方法など様々な統計的方法が、機械学習や統計学などの分野で提案され、利用されている。とくに機械学習の分野では、画像、音声、脳波、Webテキストデータなどの大規模データを計算機で効率的に統計処理するための方法が研究され、最適化やアルゴリズムなど計算機科学の諸分野と深く関連している。私自身は「推論」と「計算」の両面に興味を持ちつつ研究をすすめている。
■研究テーマ■
(1) 学習アルゴリズムの開発
機械学習の分野では、予測精度の高い学習アルゴリズムの開発や理論的解析が行われている。とくに近年、ブースティングと呼ばれるアンサンブル学習法の一種が注目されている。ブースティングとは予測精度が低い「弱学習アルゴリズム」を用いて、予測精度が高い推定アルゴリズムを構成する学習方法である。ここでいう弱学習アルゴリズムとは、予測精度は低いが計算スピードは非常に速い学習アルゴリズムを指し、二分木などを用いる推定方式として実装されている。数理統計学の観点からすれば、ブースティングは一般化線形モデルの重み付き最小二乗法による推定方法と関連があり、また最適化の観点からは関数空間における座標降下法とみなすことができる。このようにブースティングは周辺のさまざまな研究分野と関連を持っている。さらに遺伝子データ解析などにブースティング法が応用され、ある疾患に関連した遺伝子を同定するなどの成果を挙げている。
学習法として広く応用されているブースティング法であるが、いくつか実用上の問題点がある。とくに外れ値のように大きなノイズが加わるような状況では、データによって推定結果が大きく変わってしまい、信頼性のある予測が困難になる。このような問題点を踏まえ、ブースティング法を外れ値に対してロバスト化する研究をすすめ、成果を得ている。
(2) 情報幾何
多くの統計的推論では、統計モデルを設定して推論をおこなう。このとき統計モデルの幾何学的な性質が、推定量の推定精度と密接に関連している。統計モデルを可微分多様体として捉えて、推定量の統計的性質と統計モデルの幾何的な関係を微分幾何的な方法を用いて研究するのが、情報幾何の特徴である。情報幾何では従来のリーマン幾何学とは若干異なり、接続の双対性という構造が情報量に対する不変性から自然に導かれる。データがもつ本質的な情報量を接続の双対性によって捉えることができ、推定量の推定精度が統計モデルの双対接続に関する曲率を通して理解される。このような幾何学的な見方をすることで、高い推定精度を実現する推定量の特徴を直感的に理解することができ、実際に推定量を構成する上でも大いに役に立つ。
現在、ブースティング法のアルゴリズムを直感的に理解するための枠組として、情報幾何を応用した研究を進めている。その他にも、さまざまな学習方法を情報幾何の観点から眺め、推定精度の向上やアルゴリズムの計算効率の改善のための指針としている。
(3) 不確実性のもとでの最適化と機械学習
近年最適化の分野で、不確実性のもとでの最適化が重要視されている。最適化問題が線形計画法のような形式で与えられたとき、そこに含まれる係数が不確定でノイズを含んでいることもある。現在、機械学習と不確実性のもとでの最適化との関連について研究を進めている。
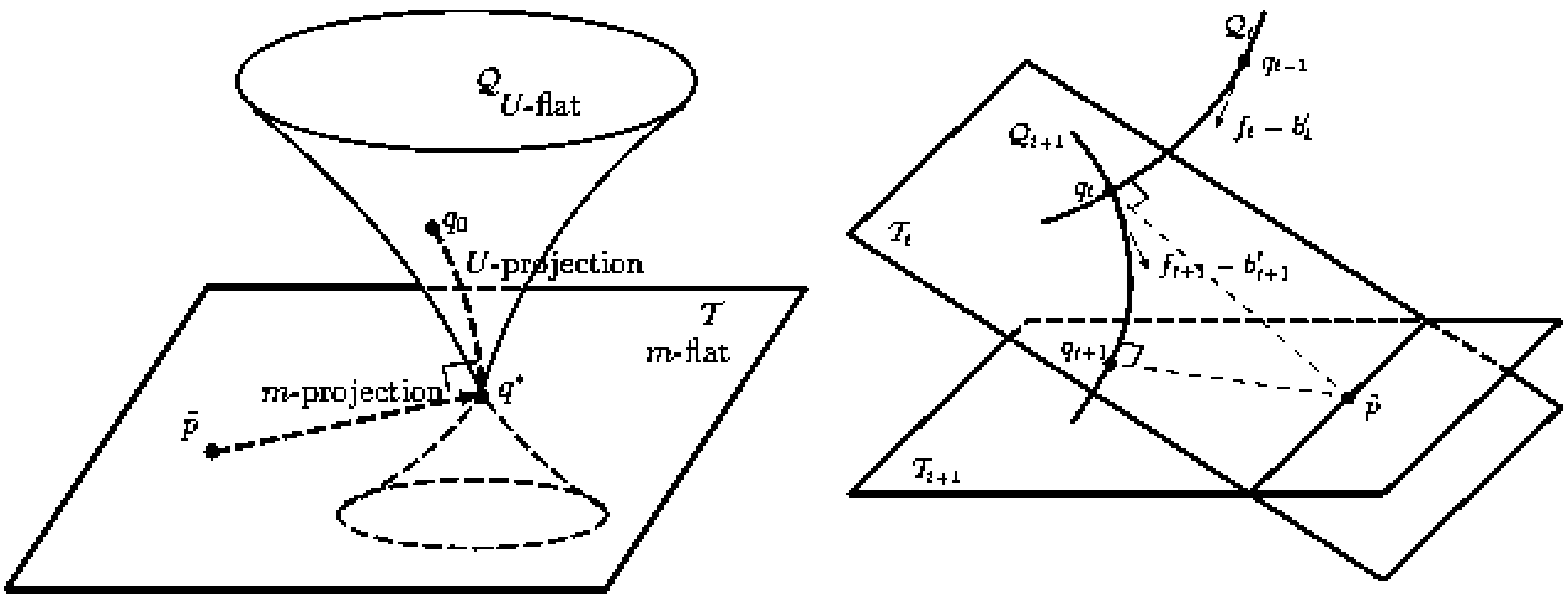
ブースティングの情報幾何構造
経歴
- 2001年 東京工業大学情報理工学研究科助手
- 2007年 名古屋大学情報科学研究科准教授
- 2016年 名古屋大学情報科学研究科教授
所属学会
- 電子情報通信学会
- 日本統計学会
主要論文・著書
- Robust Estimation under Heavy Contamination using Unnormalized Models. Biometrika, 2015.
- Empirical Localization of Homogeneous Divergences on Discrete Sample Spaces. The Neural Information Processing Systems (NIPS), 2015.
- Density Ratio Estimation in Machine Learning, Cambridge University Press 2012.
- 統計的学習理論 (機械学習プロフェッショナルシリーズ),講談社,2016.
- パターン認識 (Rで学ぶデータサイエンス 5),共立出版,2009.











