Comprehensive List of Researchers "Information Knowledge"
Department of Information Engineering
- Name
- ISHII, Katsuya
- Group
- Information Network Systems Group
- Title
- Professor
- Degree
- Dr. of Science
- Research Field
- Simulation of various vortical flows / Parallel computing / Grid computing

Current Research
Computational Fluid Dynamics & Parallel Computing
OUTLINEOur field of research is large-scale parallel computing in the area of numerical algorithms. This research is closely related to fluid physics. Our studies focus on large-scale parallel computing for the various phenomena in fluid dynamics. Numerical studies of vortical flows near solid bodies require high accuracy and high resolution, since there are vortices with different spatial scales in these regions, and complicated nonlinear interactions are observed near the separation points and the wake in these flows. We investigate various vortical flow phenomena through large-scale numerical simulations using supercomputers as well as by employing numerical schemes for high-performance computation with better accuracy and greater resolution. Our research topics are as follows.
TOPICS
- Numerical analysis of vortex shedding mechanisms at different Reynolds numbers. Such phenomena are observed in incompressible flows past bluff bodies and/or the flow past 2-D wings with a high angle of attack.
- Incompressible vortical flow fields in three-dimensional lid-driven cavities at different Reynolds numbers and different aspect ratios. These flow fields are simple models of a short-dwell coater.
- Numerical estimation of aerodynamical sound and numerical investigation of the sound source phenomena in the flow past wings and in induced flows due to the interaction of two vortex rings. These are basic studies of fan noise and/or noise of high-speed vehicles.
- Numerical investigation of 3D motions of gas bubbles in liquids and/or interfaces using a three-dimensional level set approach.
- Numerical analysis of blood flows in/near aneurysms in arteries of the brain. The development and implementation of effective numerical schemes with greater accuracy and higher resolution using high-performance computation is another research subject.
- Study of finite difference schemes with high accuracy and spectral-like resolution, i.e. the vector-potential method, efficient compressible schemes, and combined compact schemes. In addition, the development and effective implementation of parallel algorithms is also investigated using SIMD and MIMD computers.
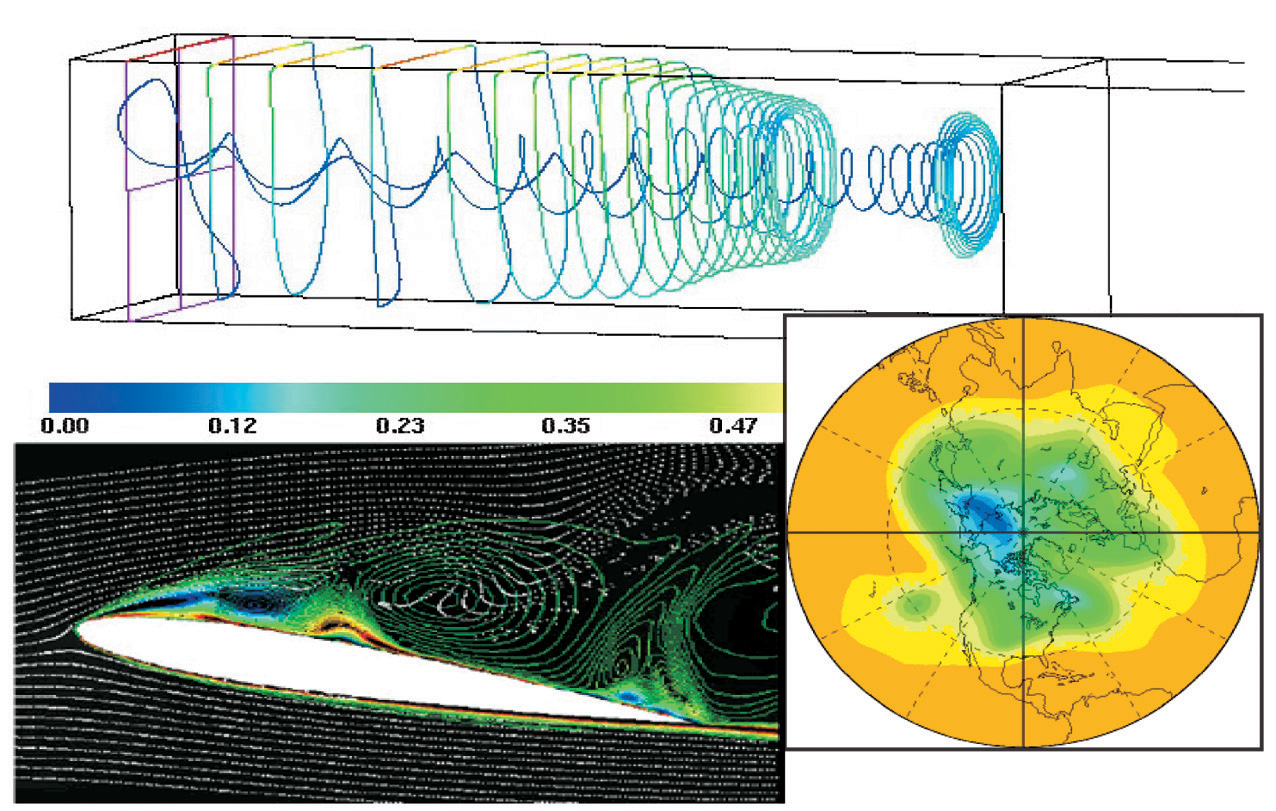
Figure : Results of various flow simulations
Career
- Katsuya Ishii received his Dr. of Science degree in physics from Tokyo University in 1980.
- He was an Assist. Prof. at the University of Tokyo from 1980-1987, Head of Research of ICFD, Co. from 1987 -1995, and an Assoc. Prof. at the Dept. of CSE, Nagoya Univ. from 1995-2002.
- Since 2002, he has been a Prof. at the Information Technology Center, Nagoya University.
Academic Societies
- JSFM
- JPS
- APS
- AIAA
- SIAM
- JSIAM
- JSME, ASJ
Publications
- “Accurate Numerical Simulation of Three-dimensional Lid-driven Cavity Flows with Different Span Lengths,” Vortex-Dominated Flows, pp. 87-98, World Scientific (2005).
- Flow Simulation using Combined Compact Difference Scheme with Spectral-like Resolution, New Developments in Computational Fluid Dynamics, pp. 256-260, Springer (2005).
- Fat Solver of the Shallow Water Equations on a Sphere using a Combined Compact Difference Scheme, Journal of Computational Physics, 187, pp. 639-659 (2003).








