Comprehensive List of Researchers "Information Knowledge"
Department of Computer Science and Mathematical Informatics
- Name
- SAKAI, Masahiko
- Group
- Theory of Computation Group
- Title
- Professor
- Degree
- Dr. of Engineering
- Research Field
- Term rewriting systems / Program transformation / Automatic theorem proving

Current Research
What is the meaning of programs ?
It is well-known that creating correct programs is difficult because basically “no programs without bugs”.First, the semantics of programming language must be mathematically formalized for correct programs. Currently we are studying the basic properties that programs must satisfy, which include strategies for efficient computation, the framework and basic techniques for automatically proving the properties of programs, and equivalent program transformation techniques for obtaining efficient programs. We aim to develop software creation schemas for obtaining highly reliable and efficient programs.
・Term rewriting : a mathematical program model
A term rewriting system is a set of rules, which defines reduction on expressions, for instance 0+x → x. This can be regarded as a programming model by capturing a given term as an input and the term obtained by reduction as output. Although term rewriting systems are simple models, their computability is identical to other computer languages. We are studying not only term rewriting systems but also their extensions with higher-order functions that treat functions as data and with priorities on rules, which are the gaps for applying systems to the analysis of functional program languages.
- Computation strategy studies
In declarative programming languages, we sometimes encounter cases in which we cannot reach a solution by a specific order of computation even though it exists. Our research clarifies algorithms that show where computation is needed for obtaining the solution and the conditions under which the algorithms work correctly. More specifically, we study theoretical aspects and applications for sequential computation strategies for term and priority term rewriting systems.
- Study of computation termination
It is important to clarify the sufficient conditions that guarantee the termination of programs since it is undecidable. Such conditions are indispensable in the K-B completion algorithm, which is valuable for program transformation and automatic theorem proving. We study termination conditions for term rewriting systems with/without higher-order functions.
・Program transformation and/or generation
Program understandability and correctness are incompatible with program efficiency. We study program transformation that generates the latter from the former. We also study frameworks for the automatic generation of programs that implement inverse computation and that satisfy the properties we require.
・Specification verification and automatic theorem proving
To obtain a program from non-executable requirement specifications, it is necessary to transform the given one into an executable one by giving implementation information. Since this transformation, called an implementation, is impossible without human intervention, a verification process is needed for correctness. We are studying formalization and a supporting method for verification. We are also trying safety verification of security protocols.
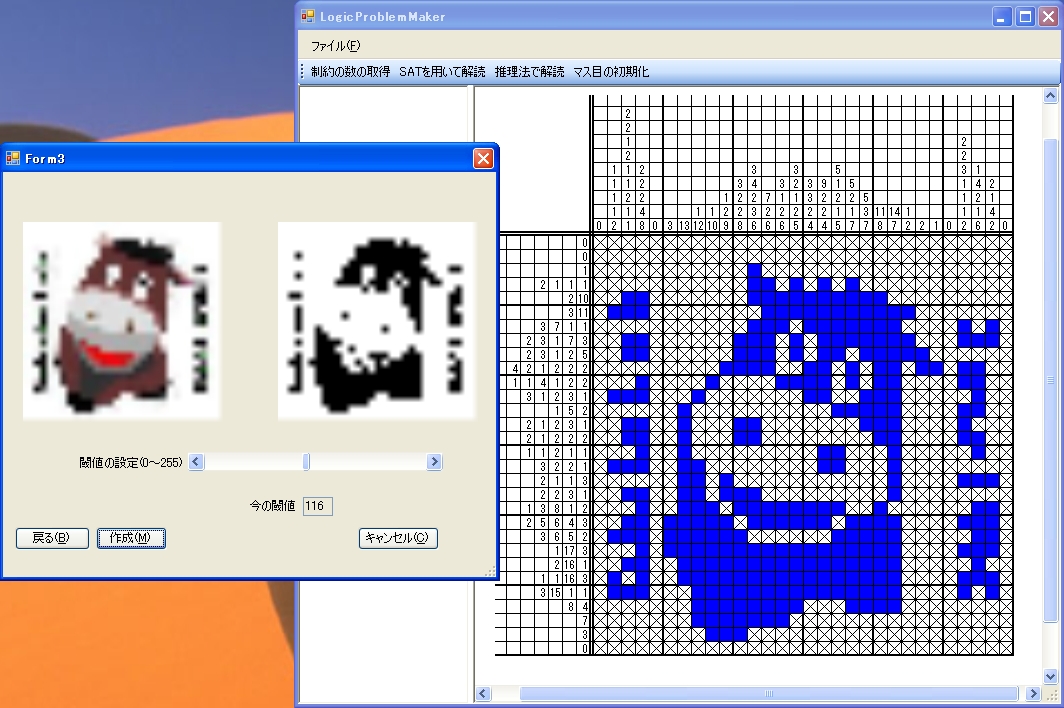
Figure : Puzzle creation tool for picture logic by SAT solving
Career
- Completed graduate course at Nagoya University in 1989.
- Assistant professor at Nagoya University from 1989.
- Associate professor at JAIST, Hokuriku from 1993.
- Associate professor at Nagoya University from 1997.
- Professor at Nagoya University from 2002.
Academic Societies
- The Institute of Electronics Information and Communication Engineers
- Japan Society for Software Science and Technology
Publications
- Algebraic Specification and Automatic Generation of Compilers, Trans. IEICE, Vol. J73-D-I, No. 12, 1990 (in Japanese).
- Semantics and Strong Sequentiality of Priority Term Rewriting Systems, Theoretical Computer Science, Vol. 208, No. 1-2, 1998.
- On Dependency Pair Method for Proving Termination of Higher-Order Rewrite Systems, IEICE Trans. on Information and Systems, Vol. E88-D, No. 3, 2005.








